Définition : Une figure géométrique est dite symétrique si il est possible de la superposer à elle-même par une opération de symétrie. Il existe trois opérateurs de symétrie.
Centre de symétrie (C) : Une figure géométrique possède un centre de symétrie si chaque face est reproduite par une même face identique et parallèle sur le côté opposé. Le centre correspond à l’intersection des axes et des plans de symétrie.
Plan de symétrie (ou miroir) (M) : Un plan de symétrie est un miroir qui fait correspondre tout point A de la figure géométrique un autre point A’ situé sur la normal à ce plan passant par A. A et A’ sont équidistants du plan.
Axe de symétrie (A) : Une droite est un axe de symétrie d’ordre n lorsqu’il est possible de faire tourner la figure géométrique autour de cette droite d’un angle équivalant à 360° et que la figure se retrouve confondue avec elle-même. En minéralogie, on rencontre des axes d’ordre 2, 3, 4 et 6.
Cet article est complémentaire avec l’article sur la géométrie des systèmes cristallins.
Symétrie du système cubique
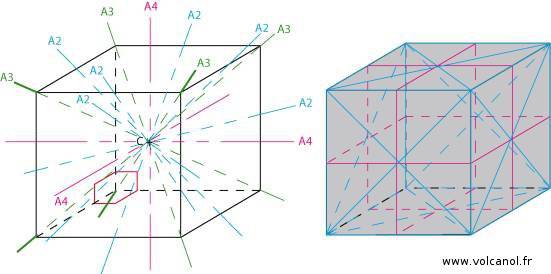
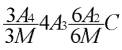
Rappels des caractéristiques de la maille
a=b b=c a=c
α=90° β=90° γ=90°
Symétrie du système quadratique
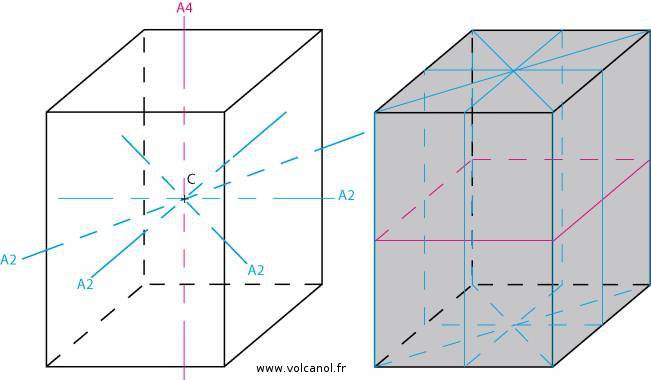
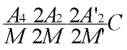
Rappels des caractéristiques de la maille
a=b b≠c a≠c
α=90° β=90° γ=90°
Symétrie du système orthorhombique
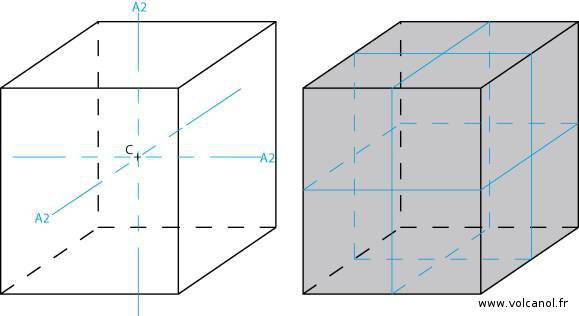
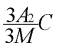
Rappels des caractéristiques de la maille orthorhombique
a≠b b≠c a≠c
α=90° β=90° γ=90°
Symétrie du système monoclinique
Rappels des caractéristiques de la maille monoclinique
a≠b b≠c a≠c
α=90° β≠90° γ=90°
Symétrie du système triclinique
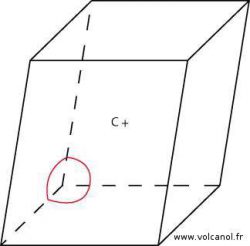
![]()
Rappels des caractéristiques de la maille triclinique
a≠b b≠c a≠c
α≠90° β≠90° γ≠90°
α≠β
Symétrie du système rhomboédrique
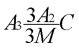
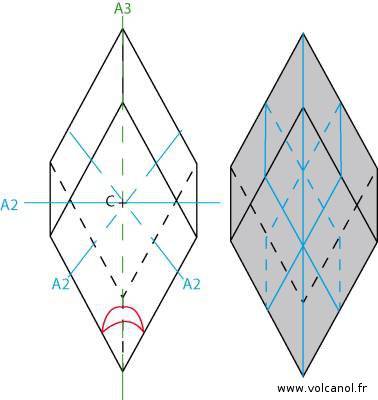
Rappels des caractéristiques de la maille rhomboédrique
a=b b=c a=c
α≠90° β≠90° γ≠90°
α=β=γ
Symétrie du système hexagonal
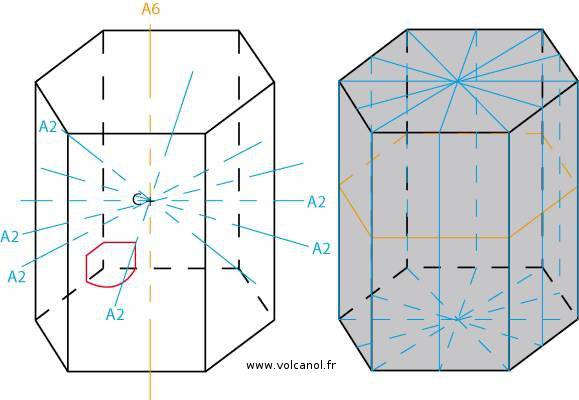
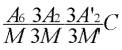
Rappels des caractéristiques de la maille
a=b b≠c a≠c
α=90° β=90° γ=120°
Voir les commentaires
merci pour votre explication ça ma beaucoup aider
Quelles sont les methodes pourra t_on utiliser pour répresenter les sept systemes cristallins.Merci cordialement
e ne comprend pas très bien la détermination des formes cristallines de chaque système
j’aimerais par quoi on commence concernant les symetries au fait je veux savoir que signifie le 1er A, le second et le 3. merci d’avance
Merci,les illustrations sont assez claires
j’aime la géologie surtout la cristallographie mais une difficulté comment retrouver le système sur un modèle
bonjour pouvez vous m indiquer des methodes faciles pour tracer les axes,les plans des septs systemes cristallins
je voudrais savoir pourquoi le système triclinique n’a pas d’axe de symetrie.merci encore
je voulais que vous mentionniez ce que signifie chaque parametre pour la bonne comprehension des debutants en geologie ainsi que les divisions des termes precisement.
je ne comprend pas les angles du système monoclinique?
salut je veut donner un methode simple pour trouver les systeme cristallin bon : 1-en prendre un systeme triclinique a≠b≠c α≠β≠γ≠90 et a chaque fois on va varie un parametre . par exempe si on prend γ=α=90° EN TROUVE LE SYSTEME MONOCLINIQUE par exemple pour trouver le systeme rhomboedrique on fait dilater un cube suivant l’axe A3 ; donc on a varie tout les ongle de la cube avec meme degre c.a.d α=β=γ≠90° de la meme manier pour quadratique on fait dilater le cube suivant l’axe A4 c.a.d on a varier seulment le parametre C …MERCI
vraiment merci les dessins sont très clairs ca m’a beaucoup aidé à comprendre mon cours!
salut mais suivant quelle voie on les construit?
Merci pour cette information intéressante
salut,pouvez nous indiquer une méthode simple pour retrouver les 7 systèmes cristallins.
pouvez vous m’indiquer a une méthode facile pour dessiner les axes de symétries?
Merci
Comment construire ces 7 systèmes cristallins ?
Bonjour, pouvez nous indiquer une méthode fixe pour retrouver toutes les symétries des sept systèmes cristallins? Merci de répondre à ma question
j’ai vu sur internet que le système orthorhombique avait les paramètres linéaires suivants a#b#c. est-ce vrai? veuillez me repondre s’il vous plais .merci et à très bientôt.
Oui cela est vrai. Le paramètre a est différent de b qui lui même est différent de c. Les 3 angles alpha, bêta et gamma sont quant à eux des angles droits (90°).
Merci et j’adore cette théorie