La géométrie des sept systèmes cristallins

Un minéral est constitué par la répétition d’un motif géométrique selon un réseau cristallin infini. Ce réseau est composé par la juxtaposition de parallélépipèdes jointifs identiques. Ces parallélépipèdes de bases sont appelés maille.

Les mailles peuvent être définies par les abngles entre les 3 axes et par les longueurs de ces axes. La convention est la suivante :

  • L’angle α se mesure entre OY et OZ, l’angle β se mesure entre OX et OZ et l’angle γ se mesure entre OX et OY.
  • La longueur de l’arête la maille élémentaire a se mesure sur l’axe OX, la longueur b sur l’axe OX et la longueur c sur l’axe OZ.

Les sept systèmes cristallins

Pour l’ensemble des minéraux, il n’existe que sept mailles élémentaires différentes.

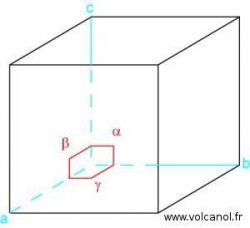
Le système cubique

a=b b=c a=c
α=90° β=90° γ=90°

Système cubique

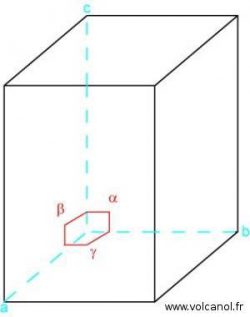
Le système quadratique

a=b b≠c a≠c
α=90° β=90° γ=90°

Système quadratique

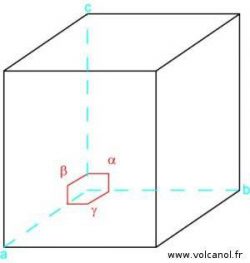
Le système orthorhombique

a≠b b≠c a≠c
α=90° β=90° γ=90°

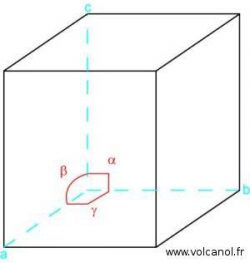
Le système monoclinique

a≠b b≠c a≠c
α=90° β≠90° γ=90°

Système monoclinique

Le système triclinique

a≠b b≠c a≠c
α≠90° β≠90° γ≠90°
α≠β

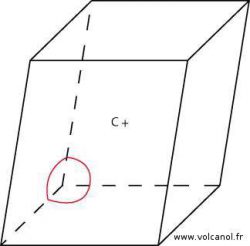
Symétrie du système triclinique

Le système rhomboédrique

a=b b=c a=c
α≠90° β≠90° γ≠90°
α=β=γ

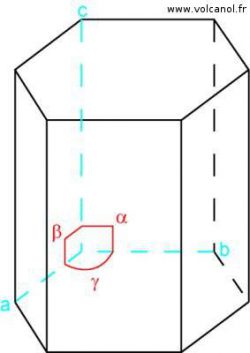
a=b b≠c a≠c
α=90° β=90° γ=120°

Système hexagonal

Après la lecture de cet article au sujet de la géométrie des systèmes cristallins, n’hésitez pas à consulter l’article portant sur la symétrie de ces systèmes cristallins.

1 Star2 Stars3 Stars4 Stars5 Stars6 Stars7 Stars8 Stars9 Stars10 Stars (No Ratings Yet)
Loading...

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Voir les commentaires