This website uses cookies so that we can provide you with the best user experience possible. Cookie information is stored in your browser and performs functions such as recognising you when you return to our website and helping our team to understand which sections of the website you find most interesting and useful.
A mineral is constituted by the repetition of a geometrical pattern according to an infinite crystal lattice. This lattice is composed by the juxtaposition of identical parallelepipeds. These basic parallelepipeds are called meshes.
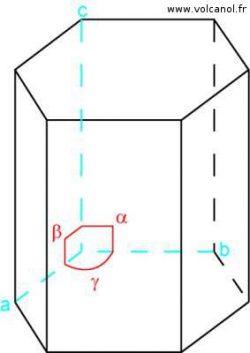
Meshes can be defined by the abngles between the 3 axes and by the lengths of these axes. The convention is as follows:
- Angle α is measured between OY and OZ, angle β is measured between OX and OZ and angle γ is measured between OX and OY.
- The length of the edge of the elementary mesh a is measured on the OX axis, the length b on the OX axis and the length c on the OZ axis.
The seven crystal systems
For all minerals, there are only seven different elemental meshes.
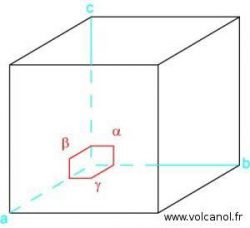
The cubic system
a=b b=c a=c
α=90° β=90° γ=90°
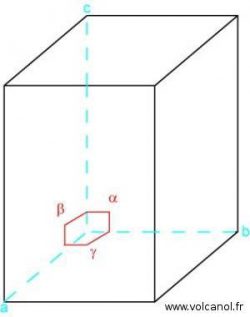
The quadratic system
a=b b≠c a≠c
α=90° β=90° γ=90°
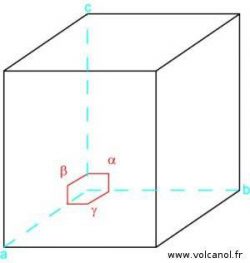
The orthorhombic system
a≠b b≠c a≠c
α=90° β=90° γ=90°
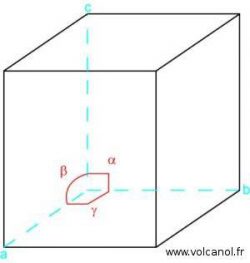
The monoclinic system
a≠b b≠c a≠c
α=90° β≠90° γ=90°
The triclinic system
a≠b b≠c a≠c
α≠90° β≠90° γ≠90°
α≠β
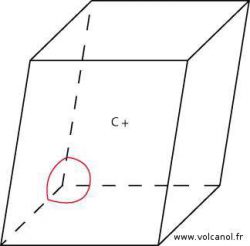
The rhombohedral system
a=b b=c a=c
α≠90° β≠90° γ≠90°
α=β=γ
a=b b≠c a≠c
α=90° β=90° γ=120°
After reading this article on the geometry of crystal systems, please feel free to consult the article on the symmetry of crystal systems.
(No Ratings Yet)
Loading...Comments are closed here.